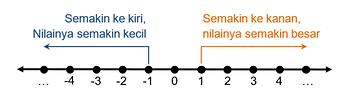
Bilangan Bulat dan Operasinya

Matematika SMP Kelas 7
#1

Bilangan Bulat

Bilangan bulat adalah kumpulan atau himpunan yang nilainya bulat, dan dilambangkan dengan huruf “Z”. Bilangan bulat terdiri dari bilangan cacah dan bilangan bulat negatif, istilah lain dari bilangan cacah yaitu: gabungan bilangan bulat positif (bilangan asli) dan nol. perhatikan gambar dibawah ini!

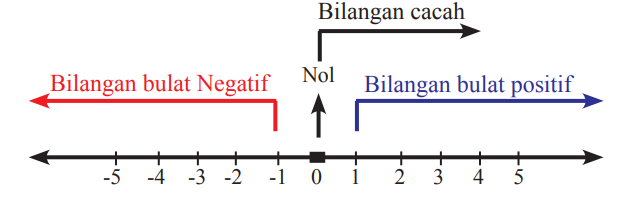
Bilangan

Adapun bilangan lainnya yang berada didalam bilangan bulat, diantaranya:

Bilangan ganjil

Bilangan ganjil adalah himpunan bilangan asli yang nilainya tidak habis dibagi dua.
Contohnya:
A=\{1,3,5,7,...\}

Bilangan genap

Bilangan genap adalah himpunan bilangan asli yang nilainya habis dibagi dua, kebalikan dari bilangan ganjil.
Contohnya:

B=\{2,4,6,8,10,..\}

Bilangan prima

Bilangan prima adalah himpunan bilangan asli yang lebih dari 1 dan hanya bisa dibagi dengan angka 1 atau bilangan itu sendiri.
Contohnya:

A=\{2,3,5,7,...\}

Bilangan komposit

Bilangan komposit adalah himpunan bilangan asli yang lebih dari 1, tetapi tidak termasuk bilangan prima.
Contohnya:
B=\{4,6,8,9,...\}

Membandingkan bilangan

Dalam membandingkan bilangan bulat, kalian perlu tahu terlebih dahulu urutan dalam bilangan bulat. Mengurutkan bilangan bulat berarti menuliskan bilangan bulat secara urut dari nilai terkecil ke nilai terbesar, atau sebaliknya.

A
A1054×283 55.4 KB

Nah, setelah mengetahui urutannya kita dapat membandingkan bilangan bulat tersebut. Membandingkan bilangan bulat berarti menentukan nilai suatu bilangan bulat apakah lebih besar, sama dengan, atau lebih kecil dari bilangan bulat lainnya.
Misalkan, a dan b termasuk dalam himpunan bilangan bulat, maka

  • Jika a lebih besar dari b, maka a > b

  • Jika a sama dengan b, maka a = b

  • Jika a lebih kecil dari b, maka a < b

Contoh:

  1. -4 < 1
  2. 5 > 3
  3. 2 = 2

Operasi bilangan bulat

Penjumlahan dan sifatnya

Salah satu rumus penting; a + (-b)=a-b

Contoh:

7+(-10)= 7-10=3

Sifat-sifat penjumlahan

a. Komutatif; a+b = b+a

  • 5+3 = 3+5

b. Asosiatif; (a+b)+c = a+(b+c)

  • (2+5)+3 = 2 + (5+3)

c. Tertutup; misal a dan b bilangan bulat, maka (a + b) juga merupakan bilangan bulat.

d. Memiliki identitas; a+0 = a, 0 disebut identitas penjumlahan

e. Invers penjumlahan; a+(-a)=0, maka (-a) disebut invers penjumlahan a.

Pengurangan

Pengurangan merupakan kebalikan dari penjumlahan.

Contoh:
8 -(-2) = 8+2 =10\\ 3-(-3)= 3+3=6\\ 2-7 = -5

Perkalian dan sifatnya

Catatan:

x

x
x882×181 14.7 KB

Contoh:

3 \times (-2) = (-2) \times (-2) \times (-2) = -6

(-2) \times (-2) = 2 \times 2 = 4

Sifat-sifat perkalian

Untuk setiap bilangan bulat a,b dan c berlaku:

  1. Sifat tertutup \to a \times b = c

  2. Sifat komutatif \to a \times b = b \times a

  3. Sifat asosiatif \to (a \times b)\times c = a \times (b \times c)

  4. Sifat distributif perkalian terhadap penjumlahan
    a \times (b+c) = (a \times b) + (a \times c)

  5. Sifat distributif perkalian terhadap pengurangan
    a \times (b-c) = (a \times b) - (a \times c)

  6. Unsur identitas \to a\times 1 = 1\times a = a, bilangan 1 disebut unsur identitas.

  7. Perkalian dengan Nol \to a \times 0 = 0 atau (-a) \times 0 = 0

Pembagian

Operasi pembagian bilangan bulat merupakan kebalikan dari operasi perkalian.
Jika a, b, dan c adalah bilangan bulat dan b ≠ 0 maka a : b = c jika dan hanya jika a = b × c.

Operasi pembagian bilangan bulat dapat dinyatakan dalam beberapa bentuk, di antaranya adalah sebagai berikut:

image

Bentuk pembagian di atas dapat digunakan sesuai dengan kebutuhan.
Mengingat pembagian merupakan kebalikan dari perkalian, maka dapat dituliskan sebagai berikut.

a × b = c ⇔ c : a = b atau c : b = a

Silahkan perhatikan tabel dibawah ini!

image
image760×229 12.6 KB

Dari data-data perhitungan pada tabel di atas, maka dapat kita ambil beberapa pola tanda pada pembagian bilangan bulat berikut ini.

a. (+) : (+) = (+)

b. (+) : (−) = (−)

c. (-) : (+) = (−)

d. (−) : (−) = (+)

image
image889×175 11.9 KB

Sifat - sifat pembagian

  1. Tidak bersifat tertutup
    Untuk setiap bilangan bulat a dan b, jika a : b = c, maka c belum tentu merupakan bilangan bulat.

    Contoh:

  • 4 : 3 = 1,3333\to bukan bilangan bulat

  1. Tidak bersifat komutatif
    Hasil pembagian bilangan bulat tidak pernah sama ketika letak bilangan ditukar. Sifat pembagian seperti ini disebut sifat anti komutatif dan ditulis a : b ≠ b : a

    Contoh:

  • 20 : (−10) = −2

  • 10 : 20 = −0,5

    20 : (−10) ≠ −10 : 20

  1. Tidak bersifat Asosiatif
    Hasil pembagian bilangan bulat tidak pernah sama ketika elemen-elemennya dikelompokkan dengan cara yang berbeda. Sifat pembagian seperti ini disebut sifat anti asosiatif dan ditulis (a : b) : c ≠ a : (b : c)

  2. Tidak bersifat distributif
    Pada operasi pembagian bilangan bulat, tidak berlaku sifat distributif (penyebaran). Secara umum, untuk a, b dan c bilangan bulat, maka:
    a : (b + c) = (a : b) + (a : c)\\ a : (b − c) = (a : b) − (a : c)

  3. Pembagian bilangan bulat dengan nol
    Untuk setiap bilangan bulat a, a : 0 tidak terdefinisi.

  4. Pembagian bilangan bulat oleh nol
    Untuk setiap bilangan bulat a, berlaku 0 : a = 0.

Silahkan jika ada yang mau bertanya dan berdiskusi. Terima kasih.

1 Likes