Fungsi Komposisi (Fungsi Bersusun)

[annisa]

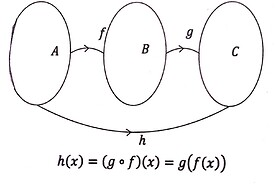
Definisi Fungsi Komposisi

Diberikan dua fungsi dengan aturan f suatu fungsi dari A ke B (f: A\to B) dan g suatu fungsi dari B ke C (g: B\to C), maka h fungsi dari A ke C disebut komposisi fungsi dan dinyatakan g(f(x)) atau g \circ f yang ditentukan oleh:

Fungsi komposisi g \circ f dari A ke C apabila f: A\to B dan g: B\to C dengan R(f)\cap D(g) \neq \phi. Maka daerah definisi D(g \circ f) = {x \in A|f(x) \in R(f)\cap D(f)}. Apabila digambarkan akan terlihat seperti gambar berikut ini:

D(g \circ f) = {x in A|f(x) in R(f) \cap D(g)}
Dengan cara yang sama,

D(f \circ g) = {x\in A|f(x) \in R(g) \cap D(f)}

Catatan: pada umumnya D(f \circ g) \neq D(g \circ f)

Contoh:

Diketahui f(x) = 2x+5 dan g(x) = \sqrt{x-1}

Tentukan:
a. (g\circ f)(x) dan D(g \circ f)

b. (f\circ g)(x) dan D(f \circ g)

Jawab:

\begin{align} a). (g\circ f)(x) &= g(f(x))\\ &=g(2x+5)\\ &=\sqrt{(2x+5)-1}\\ &=\sqrt{(2x+4}\\ R(f) &= ℝ\\ D(g) &= \{x|x\geq 1\}\\ D(g \circ f) &=\{x|x\geq 1\} = [1,\infty) \end{align}

\begin{align} b). (f\circ g)(x) &= f(g(x))\\ &=f(\sqrt{x-1})\\ &=2\sqrt{x-1} + 5\\ R(g) &= \{y|y\geq 0\}\\ D(f) &= ℝ\\ D(f \circ g) &=\{y|y\geq 0\} = [0,\infty) \end{align}

Silahkan jika ada yang ingin bertanya dan berdiskusi. Terima kasih