FUNGSI KOMPOSISI
- Pengertian Fungsi Komposisi
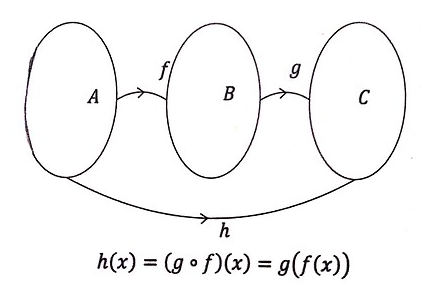
Fungsi komposisi adalah operasi di mana dua fungsi digabungkan untuk membentuk fungsi baru. Jika terdapat dua fungsi f : A \to B dan g : B \to C, maka fungsi komposisi dari f dan g adalah h(x) = (g \circ f)(x) = g(f(x)), yang berarti:
-
Fungsi f(x) pertama-tama memetakan elemen dari A ke B
-
Fungsi g(x) kemudian memetakan hasil dari f(x) (yang berada di B) ke C
Dengan kata lain, fungsi f diterapkan terlebih dahulu, dan kemudian hasilnya digunakan sebagai masukan untuk fungsi g. jadi urutan operasinya adalah:
\begin{align}
&&&&h(x) = g(f(x))\\
&&&&(g \circ f)(x) = g(f(x))\\
&&&&(f \circ g)(x) = f(g(x))
\end{align}
-
Contoh:
Diketahui : f(x) = 2x dan g(x) = x+3
a. Tentukan (g \circ f)(x)
b. Tentukan (f \circ g)(x)Jawab:
\begin{align}
(g \circ f)(x) &= g(f(x))\\
&= g(2x)\\
&= 2x+3
\end{align}
\begin{align}
(f \circ g)(x) &= f(g(x))\\
&= f(x+3)\\
&= 2(x+3)\\
&= 2x+6
\end{align}
- Sifat-Sifat Komposisi Fungsi
- Komposisi fungsi tidak bersifat asosiatif
(f \circ g)(x) \neq (g \circ f)(x) - Komposisi fungsi bersifat assosiatif
(f \circ (g \circ h))(x) = ((f \circ g) \circ h)(x) - Komposisi fungsi terdapat unsur identitas yaitu I(x) = x sehingga mempunyai sifat (f \circ I)(x) = (I \circ f)(x) = f(x)
Sekian. Terima kasih!