Operasi Himpunan

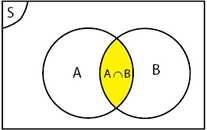
1. Irisan

Misalkan A ⊆ S dan B ⊆ S, maka:

Irisan dua himpunan A dan B adalah himpunan yang anggotanya merupakan anggota A dan anggota B, dilambangkan dengan A ∩ B

%A nn B = {x| x in A, x in B}%

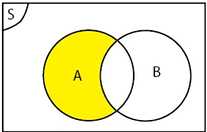
2. Himpunan Komplemen

Himpunan Komplemen A adalah himpunan bagian Semesta (S) yang anggotanya bukan anggota A atau semua anggota kecuali anggota A itu sendiri, dilambangkan dengan $\overline{A}$ atau $A^c$

%A^c= {x| x in S, x !in A}%

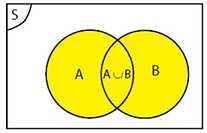
3. Gabungan

Misalkan A ⊆ S dan B ⊆ S, maka:

Gabungan dua himpunan A dan B adalah himpunan yang anggotanya milik anggota A atau anggota B, dilambangkan dengan A ∪ B

%A uu B = {x| x in A, x in B}%

4. Selisih

Selisih himpunan A dan B ditulis:

• A − B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A namun bukan anggota himpunan B.

%A - B = {x| x in A, x !in B}%

• B − A adalah himpunan yang anggota-anggotanya merupakan anggota himpunan B namun bukan anggota himpunan A

%B- A = {x| x in B, x !in A}%

5. Penjumlahan

Himpunan yang elemennya adalah elemen himpunan $A$ atau himpuna $B$ namun bukan merupakan anggota $A \cap B$ adalah hasil tambah dari himpunan $A$ dan himpunan $B$ yang ditulis $A+B$
Notasinya: %A+B = {x| x in A, x in B, x in (Ann B)}%

Contoh:

Diketahui:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4, 5} dan B = {4, 5, 6, 7, 8}

Maka:
%A uu B = {1,2,3,4,5,6,7,8}% %A nn B = {4,5}% %A-B = {1,2,3}% %B-A = {6,7,8}% %bar A = {6,7,8,9}% $\overline{A\cup B}$ = {$9$}

$A+B =$ {$1,2,3,6,7,8$}

Silahkan jika ada yang ingin bertanya dan berdiskusi. Terima kasih.