Penyelesaian SPLDV

[annisa]

Penyelesaian SPLDV

Terdapat beberapa metode dalam menyelesaikan sistem persamaan linear dua variabel.

Metode Eliminasi

Metode eliminasi yaitu metode penyelesaian dengan cara menghilangkan salah satu variabel, sehingga variabel yang tersisa dapat diketahui nilainya.
Contoh:
Misalkan diberikan sistem persamaan:

\begin{cases} 3x + 4y &= 24 \\ x+2y &= 10 \end{cases}

Eliminasi untuk menghilangkan variabel x

\begin{align} 3x + 4y &= 24|\times1|\\ x+2y &= 10 |\times3|\\ \\ \frac{3x + 4y = 24\\ 3x + 6y = 30 -}{-2y=-6\\ -y = \frac{-6}{-2}\\ y = 3 } \end{align}

Didapatkan nilai y=3, selanjutnya dilakukan eliminasi variabel y untuk mendapatkan nila x

\begin{align} 3x + 4y &= 24|\times1|\\ x+2y &= 10 |\times2|\\ \\ \frac{3x + 4y = 24\\ 2x + 4y = 20 -}{\\ x = 4 } \end{align}

Sehingga didapatkan nilai x=4, \text { dan } y = 3

Metode Substitusi

Metode substitusi dilakukan dengan cara menggantikan variabel satu dengan variabel yang lain. Pilih persamaan paling sederhana untuk disubstitusikan, perhatikan contoh dibawah ini:
Misalkan diberikan sistem persamaan:

\begin{cases} 3x + 4y &= 24...(1) \\ x+2y &= 10....(2) \end{cases}

Pilih persamaan kedua untuk disubstitusikan.

\begin{align} x+2y&=10\\ x &= 10-2y ....(3) \end{align}

Substitusikan persamaan 3 kedalam persamaan 1

\begin{align} 3x+4y&=24\\ 3(10-2y) + 4y &= 24\\ 30-6y+4y &= 24\\ 30 -2y &= 24\\ -2y &= 24-30\\ -y &= \frac{-6}{-2}\\ y &= 3 \end{align}

Substitusikan nilai y=3 kedalam persamaan 3

\begin{align} x &= 10-2y\\ x &= 10-2(3)\\ x &= 10-6\\ x &= 4 \end{align}

Sehingga didapatkan nilai x=4, \text { dan } y = 3

Metode Campuran

Metode Campuran yaitu penggabungan dari metode eliminasi dan metode substitusi.
Contoh:

Misalkan diberikan sistem persamaan:

\begin{cases} 3x + 4y &= 24 \\ x+2y &= 10 \end{cases}

Eliminasi untuk menghilangkan variabel x

\begin{align} 3x + 4y &= 24|\times1|\\ x+2y &= 10 |\times3|\\ \\ \frac{3x + 4y = 24\\ 3x + 6y = 30 -}{-2y=-6\\ -y = \frac{-6}{-2}\\ y = 3 } \end{align}

Substitusikan nilai y=3 kedalam persamaan paling sederhana

\begin{align} x+2y &= 10\\ x+2(3)&= 10\\ x +6 &= 10\\ x &= 10-6\\ x &= 4 \end{align}

Sehingga didapatkan nilai x=4, \text { dan } y = 3

Metode Grafik

Metode grafik dilakukan dengan mencari titik potong antara dua garis yang dibuat dalam koordinat cartesius.

Misalkan diberikan sistem persamaan:

\begin{cases} 2x + y &= 6 \\ 2x + 4y &= 12 \end{cases}

Tentukan titik potong pada persamaan pertama.
2x+y = 6
Jika y = 0, maka:

\begin{align} 2x + y &= 6 \\ 2x &= 6\\ x &= \frac{6}{2}\\ x &= 3 \end{align}

Jika x=0 maka:

\begin{align} 2x + y &= 6 \\ 0 + y &= 6\\ y &= 6 \end{align}

Maka titik potong pada persamaan 2x+y=6 adalah (3,0) \text { dan } (0,6)

Tentukan titik potong pada persamaan kedua.
2x+4y = 12
Jika y = 0, maka:

\begin{align} 2x+4y &= 12 \\ 2x - 0 &= 12\\ x &= \frac{12}{2}\\ x&= 6 \end{align}

Jika x=0 maka:

\begin{align} 2x+4y &= 12\\ 0 + 4y &= 12\\ y &= \frac{12}{4}\\ y &= 3 \end{align}

Maka titik potong pada persamaan 2x+4y = 12 adalah (6,0) \text { dan } (0,3)

Berikut gambar titik potong pada bidang koordinat

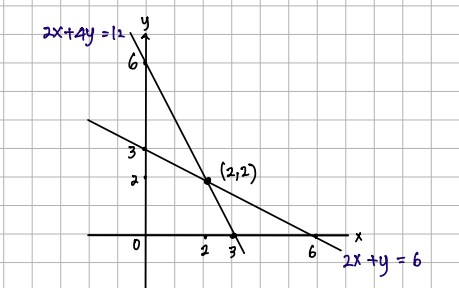
Dari gambar grafik terlihat bahwa himpunan penyelesaiannya adalah (2,2). Sehingga HP = \{ 2,2\}

Metode Determinan Matriks

Menggunakan determinan matriks untuk menyelesaikan sistem persamaan linear dua variabel

Dengan rumus umum:

\begin{align} \ ax+by &= c\\ \ dx+ey &=f \end{align}

Untuk mencari nilai x:

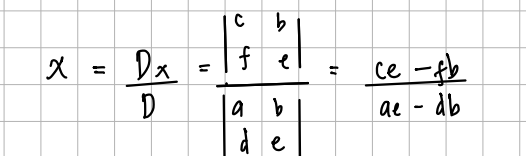
Untuk mencari nilai y:

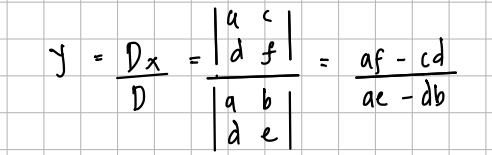
Contoh:
Misalkan diberikan sistem persamaan:

\begin{align} \ 3x+4y &= 24\\ \ x+2y &= 10 \end{align}

Sehingga akan dicari nilai x dengan determinan

Selanjutkan akan dicari nilai y dengan determinan

Dengan demikian didapat nilai x = 4, y = 3

Sekian, silahkan jika ada yang mau ditanyakan. Terima kasih!

Referensi:
Matematika Dasar_Indah Werdiningsih, S.Pd.,M.Pd.