Persamaan dan Fungsi
Pengertian Persamaan dan Fungsi
Persamaan
Persamaan adalah suatu bentuk yang menyatakan kesetaraan antara dua ekspresi matematika. Biasanya mengandung variabel yang nilainya harus dicari.
Contoh Persamaan Linear Satu Variabel:
\begin{align}
2x+3=11\\
\end{align}
Nilai x bisa dicari dengan cara:
\begin{align}
2x+3&=11\\
2x &= 11-3\\
x &= 4
\end{align}
Contoh Persamaan Kuadrat:
\begin{align}
x^2 - 5x+6=0\\
\end{align}
Penyelesaiannya bisa dengan pemfaktoran:
\begin{align}
x^2 - 5x+6&=0\\
(x−2)(x−3)&=0\\
x=2 \text{ atau } x=3\\
\end{align}
Fungsi
Fungsi adalah aturan yang menghubungkan setiap elemen dari himpunan domain (input) ke range (output) dengan aturan tertentu.
Contoh Fungsi Linear:
Jika diberikan fungsi:
\begin{align}
f(x)=2x+1\\
\end{align}
Maka jika:
- x=1, \text { maka } f(1)=2(1)+1=3
- x=2, \text { maka } f(2)=2(2)+1=5
Grafik Fungsi
Grafik Fungsi Linear
Fungsi linear berbentuk:
\begin{align}
y=ax+b\\
\end{align}
Dengan:
- a = \text{ gradien (kemiringan garis)}
- b = \text{ titik potong dengan sumbu } y
Contoh:
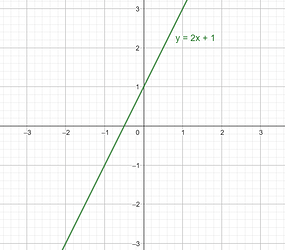
Jika y=2x+1, maka beberapa titiknya:
- Jika x=0, \text{ maka } y=1 → \text { titik } (0,1)
- Jika x=1, \text{ maka } y=3 → \text { titik } (1,3)
- Jika x=-1, \text{ maka } y=-1 → \text { titik } (-1,-1)
Berikut gambar grafiknya:
Grafiknya berupa garis lurus!
Grafik Fungsi Kuadrat
Fungsi kuadrat berbentuk
\begin{align}
y=ax^2+bx+c\\
\end{align}
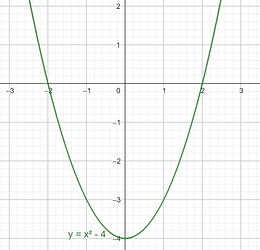
Grafiknya membentuk parabola:
- Jika a>0, parabola terbuka ke atas
- Jika a<0, parabola terbuka ke bawah
Contoh:
\begin{align}
y=x^2-4\\
\end{align}
Titik penting:
- Jika x=0, maka y=−4 (titik potong sumbu y)
- Titik puncak bisa dihitung dengan x=-\frac{b}{2a}
Latihan Soal
- Selesaikan persamaan berikut:
\begin{align}
3x-5=7\\
\end{align}
- Tentukan nilai f(3) \text { jika } f(x)=4x−2
- Buat grafik dari fungsi y=−x+2
Silahkan kerjakan dikolom komentar ya! Terima kasih!!