Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear merupakan gabungan dari beberapa pertidaksamaan linear yang dapat diperoleh penyelesaiannya.
contoh:
Diketahu pertidaksamaan:
\begin{align}
x+y &\geq4\\
2x+y &\geq 6\\
x&\geq 0\\
y&\geq0
\end{align}
Tentukan daerah penyelesaiannya!
Penyelesaian:
Menentukan titik potong pada pertidaksamaan yang pertama x+y \geq4
Untuk x = 0, maka:
\begin{align}
x+y &\geq4\\
0+y &= 4\\
y&=4
\end{align}
Untuk y=0, maka
\begin{align}
x+y &\geq4\\
x+0 &= 4\\
x&=4
\end{align}
Jadi, titik potongnya adalah (0,4) \text{ dan } (4,0)
Menentukan titik potong pada pertidaksamaan yang kedua 2x+y \geq6
Untuk x = 0, maka:
\begin{align}
2x+y &\geq6\\
2.0+y &= 6\\
y&=6
\end{align}
Untuk y=0, maka
\begin{align}
2x+y &\geq6\\
2x+0 &= 6\\
2x &=6\\
x&=\frac{6}{2}\\
x&=3
\end{align}
Jadi, titik potongnya adalah (0,6) \text{ dan } (3,0)
Kemudian digambar titik potong pada diagram cartesius
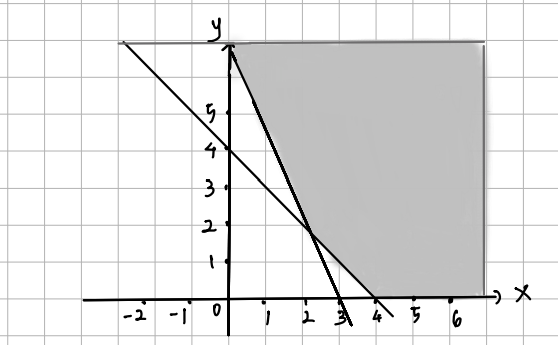
Gambar yang diarsir merupakan daerah penyelesaiannya.
Sekian, Terimakasih!