Teoram Pythagoras
Apa Itu Teorema Pythagoras?
Teorema Pythagoras adalah prinsip dalam matematika yang digunakan untuk menghitung panjang sisi segitiga siku-siku. Teorema ini berbunyi:
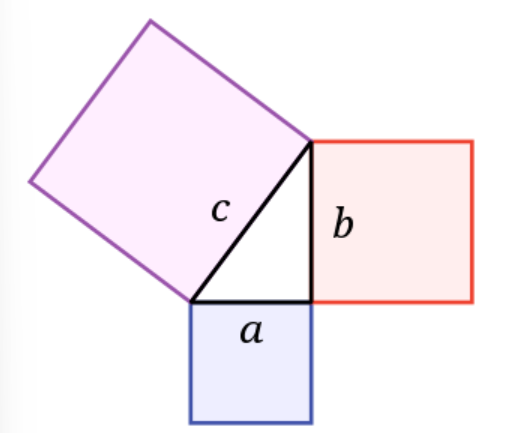
“Pada segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi lainnya.”
Secara matematis, rumusnya adalah:
\begin{align}
c^2 = a^2 + b^2\\
\end{align}
Dimana:
- c = \text{ hipotenusa (sisi miring, sisi terpanjang)}
- a= \text{ sisi tegak}
- b= \text{ sisi datar}
Contoh soal dan penyelesaian:
- Diketahui segitiga siku-siku dengan panjang sisi tegak 6 cm dan sisi datar 8 cm. Berapa panjang sisi miringnya?
Jawab:
Dengan menggunakan rumus Teorema Pythagoras:
\begin{align}
c^2 &= a^2 + b^2\\
c^2 &= 6^2 + 8^2\\
c^2 &= 36+64\\
c^2 &=100\\
c &= \sqrt{100} = 10\\
\end{align}
Jadi, panjang sisi miringnya adalah 10 cm
- Sebuah segitiga siku-siku memiliki sisi miring (hipotenusa) 13 cm dan sisi tegak lainnya 5 cm. Berapakah panjang sisi yang belum diketahui?
Jawab:
Dengan menggunakan rumus:
\begin{align}
c^2 &= a^2 + b^2\\
13^2 &= a^2 + 5^2\\
169 &= a^2 +25\\
a^2 &=169 - 25\\
a^2 &= 144\\
a &= \sqrt{144} = 12\\
\end{align}
Jadi, panjang sisi yang belum diketahui adalah 12 cm.
- Diketahui sebuah segitiga siku-siku dengan sisi miring 10 cm dan salah satu sisi tegaknya 6 cm. Hitung panjang sisi lainnya.
Jawab:
Dengan menggunakan rumus:
\begin{align}
c^2 &= a^2 + b^2\\
10^2 &= 6^2 + b^2\\
100 &= 36 + b^2\\
b^2 &=100 - 36\\
b^2 &= 64\\
b &= \sqrt{64} = 8\\
\end{align}
Jadi, panjang sisi lainnya adalah 8 cm.
Latihan Soal
- Sebuah segitiga siku-siku memiliki panjang sisi miring 25 cm dan salah satu sisi siku-sikunya 24 cm. Berapa panjang sisi lainnya?
- Sebuah tangga memiliki panjang 15 meter dan menyentuh dinding pada ketinggian 9 meter. Seberapa jauh bagian bawah tangga dari dinding?
- Jika sebuah segitiga memiliki sisi miring 20 cm dan salah satu sisinya 16 cm, hitung panjang sisi lainnya.
Silahkan kerjakan soal latihannya dikolom komentar ya!! Terima kasih!!