Trigonometri Dasar

Matematika Dasar
#1

Trigonometri Dasar

Pengertian Trigonometri

Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga. Kata trigonometri berasal dari bahasa Yunani:

  • “trigonon” (τρίγωνον) = segitiga
  • “metron” (μέτρον) = pengukuran

Perbandingan Trigonometri dalam Segitiga Siku-Siku

Dalam segitiga siku-siku, terdapat tiga perbandingan dasar yang digunakan untuk menentukan nilai trigonometri suatu sudut:

Rumus Perbandingan Trigonometri

Jika diberikan segitiga siku-siku seperti berikut:
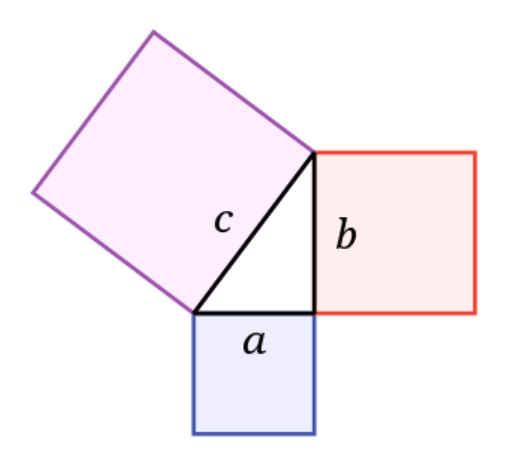
image
Dimana:

  • a= \text{ alas}
  • b=\text{ tinggi}
  • c= \text { sisi miring, sisi terpanjang}

Maka, perbandingan trigonometri didefinisikan sebagai:

  1. Sinus (sin) = \frac{\text{sisi depan}}{\text{sisi miring}}
\begin{align} \sin \theta = \frac{b}{c}\\ \end{align}
  1. Kosinus (cos) = \frac{\text{sisi samping}}{\text{sisi miring}}
\begin{align} \cos \theta = \frac{a}{c}\\ \end{align}
  1. Tangen (tan) = \frac{\text{sin}}{\text{cos}} =\frac{\text{sisi depan}}{\text{sisi samping}}
\begin{align} \tan \theta = \frac{b}{a}\\ \end{align}

Tips mudah menghafal:
SOH-CAH-TOA
DeMiSin - CosSaMi - DeSaTan

  • Sinus = Opposite / Hypotenuse (Depan / Miring)
  • Cosinus = Adjacent / Hypotenuse (Samping / Miring)
  • Tangen = Opposite / Adjacent (Depan / Samping)

Nilai Trigonometri untuk Sudut Istimewa

Beberapa sudut sering digunakan dalam trigonometri, yaitu 0°, 30°, 45°, 60°, dan 90°. Nilai trigonometri untuk sudut-sudut ini sebagai berikut:
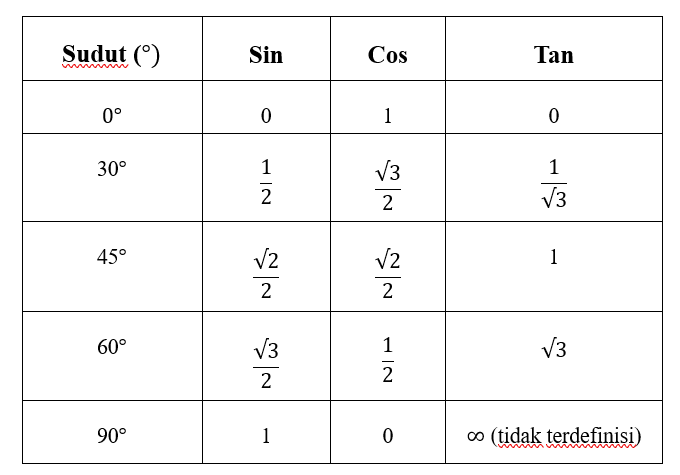
image

Cara mudah menghafal nilai sin dan cos:

  • Sinus: \frac{\sqrt{0}}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}
  • Kosinus: dibalik dari sinus

Identitas Trigonometri Dasar

Terdapat beberapa identitas trigonometri yang sering digunakan:

  1. Hubungan ** Sin, Cos, dan Tan**
\begin{align} \tan \theta = \frac{\sin \theta}{\cos \theta}\\ \end{align}
  1. Identitas Pitagoras
\begin{align} \sin^2 \theta + \cos^2 \theta &= 1\\ 1 + \tan^2 \theta &= \frac{1}{\cos^2 \theta}\\ 1+\cot^2 \theta &= \frac{1}{\sin^2 \theta} \end{align}

Contoh Soal dan Pembahasan

  1. Diketahui segitiga siku-siku dengan sisi miring 10 cm dan salah satu sudutnya 30°. Tentukan panjang sisi depan dan sisi sampingnya.
    Jawab:
  • \sin 30^\circ = \frac{\text{ sisi depan}}{\text{ sisi miring}} → \frac{1}{2} = \frac{x}{10} → x=5 \text{ cm (sisi depan)}
  • \cos 30^\circ = \frac{\text{ sisi samping}}{\text{ sisi miring}} → \frac{\sqrt{3}}{2} = \frac{y}{10} → y=5\sqrt{3} \text{ cm (sisi samping)}

Maka didapat: Sisi depan = 5 cm dan sisi samping = 5\sqrt{3}

  1. Tentukan nilai sin 45° + cos 30° - tan 60°.
    Jawab:
\begin{align} \sin 45^\circ &= \frac{\sqrt{2}}{2}\\ \cos 30^\circ &= \frac{\sqrt{3}}{2}\\ \tan 60^\circ &=\sqrt{3}\\ \end{align}
\begin{align} \sin 45^\circ + \cos 30^\circ+\tan 60^\circ\\ \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2} -\sqrt{3}\\ =\frac{\sqrt{2}+\sqrt{3}-2\sqrt{3}}{2}\\ =\frac{\sqrt{2}-\sqrt{3}}{2}\\ \end{align}

Sekian, Terima kasih!!